Intermediate
Macroeconomics

Lecture 9

Monetary Economics

In This Lecture

• What is money?
• Monetary Intertemporal Model
• Real and nominal interest rates
• Demand for money – banks and alternative means of payment
• Neutrality of money
• Zero lower bound and quantitative easing

What is Money?

• Medium of exchange – solves double coincidence of wants problem
• Store of value
• Unit of account

Measuring the Money Supply

• M0: US currency outside the Fed + deposits of depository institutions with the Fed
• M1: M0 + travelers’ checks + demand deposits + other transactions accounts $\rightarrow$ measure of assets most widely used in private sector transactions
• M2: M1 + savings deposits + small-denomination time deposits + retail money market mutual funds

A Monetary Model

• Until now, we have studied real models, in which money played no role
• In this chapter, we introduce two assets
  • Money, which can be used to purchase goods and services or nominal bonds
  • Nominal Bonds, which returns 1+R units of money in the future period

Inflation and Interest Rate

• Inflation rate where $P$ denotes current period price level and $P^{\prime}$ denotes future period price level
$$i = \frac{P^{\prime}-P}{P}$$
• Fisher relation where $R$ denotes the nominal interest rate and $r$ denotes real interest rate
$$1+r = \frac{1+R}{1+i}$$
• Short time period approximation: $r \approx R - i$

Nominal/Real Interest Rates

• Nominal interest rate is observed rate on bonds such as US treasury bills
• From this we can calculate the corresponding real interest rate
• Calculated as nominal interest rate minus CPI rate of change
• Which one is more fundamental, real or nominal?

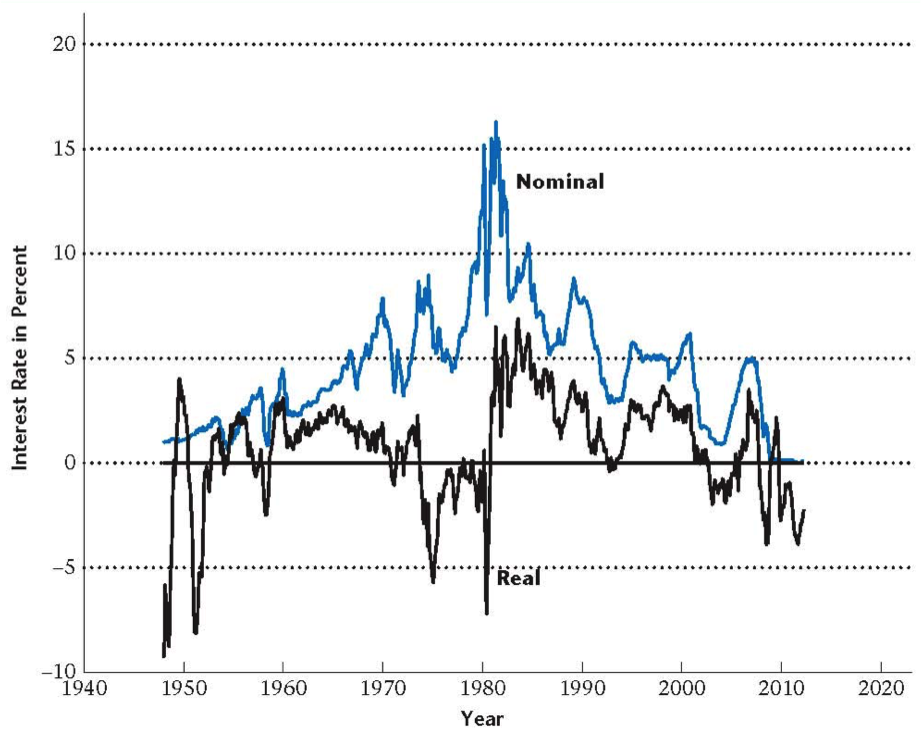
Historical Interest Rate Data

Real and nominal interest rate on 91-day US Treasury bills

Cash and Inflation

• If the nominal interest rate $R$ is higher than the rate of inflation $i$, the real return on the bond $r$ is positive
• The rate of return on money is zero – with positive inflation, the real rate of return is negative
• So then why do we hold cash?

Banks and Means of Payment

• Assume all goods must be purchased with currency or credit cards
• “Credit cards” can be assumed to stand in, more broadly, for debit cards and checks, for example – all alternative means of payment supplied by the financial system
• Goods can be purchased at price $P$, no matter what means of payment is used

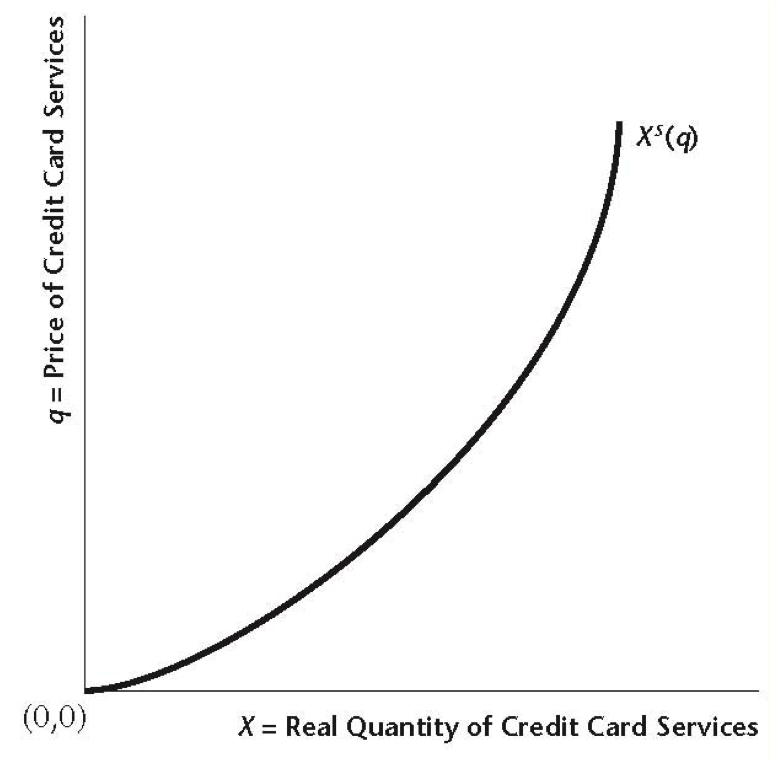
Credit Card Services

• Using a credit card costs $q$ per unit of goods purchased
• Credit supply (by banks) is given by $X^s(q)$, which is increasing in $q$
• Supplying credit card services is costly for banks

Supply of Credit Services

Profitability of extending credit balances increases as $q$ increases, so banks increase quantity supplied

Demand for Credit Services

• Quantity of goods purchased with credit card services $X^d(q)$
• Goods purchased with currency: $Y - X^d(q)$
• If for credit, marginal benefit $\gt$ marginal cost $$P(1+R) \gt P(1+q)$$ then all goods are purchased with credit cards
• Otherwise if $$P(1+R) \lt P(1+q)$$ then all goods are purchased with currency

Credit Services Equilibrium

Price of credit services is $q=R$, equilibrium amount is $X^{\ast}$

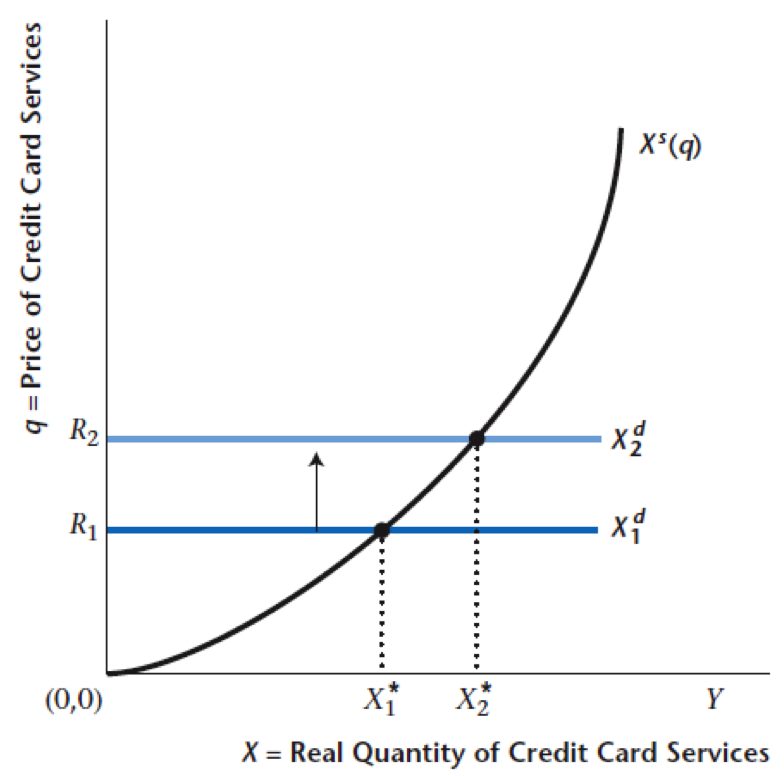
Nominal Interest Rate

Shifts the demand curve for credit services up

Equilibrium price and quantity of credit services increase

Demand for Money

• Let’s denote $X^{\ast}(R)$ as the equilibrium quantity of credit card services (increasing function of $R$)
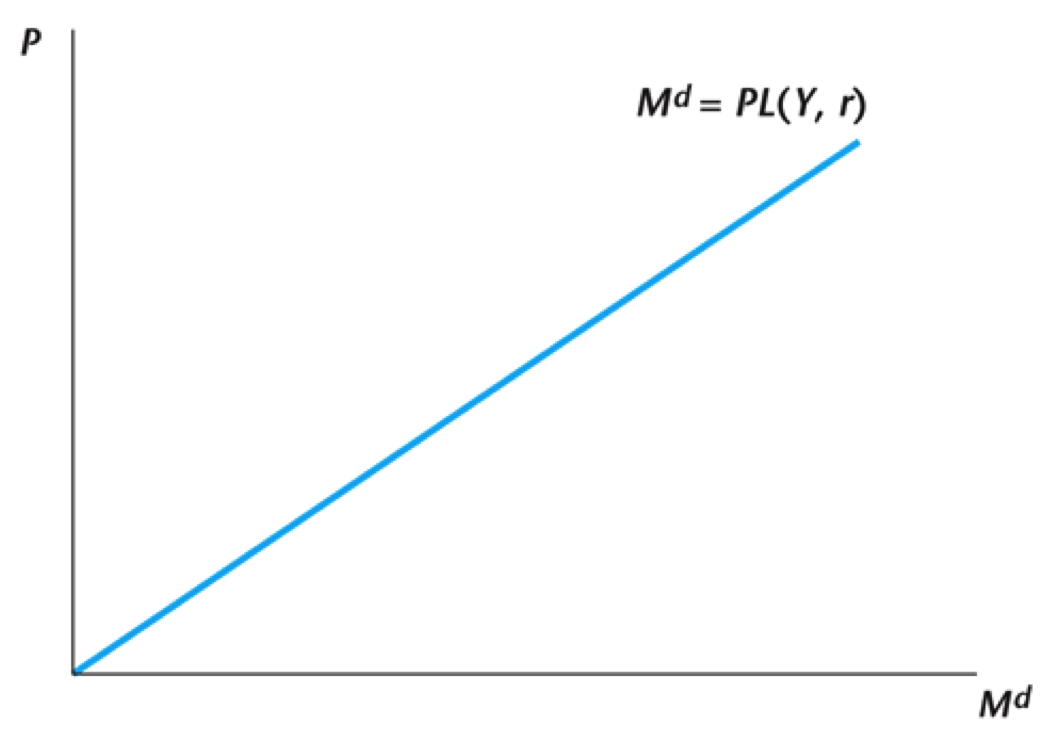
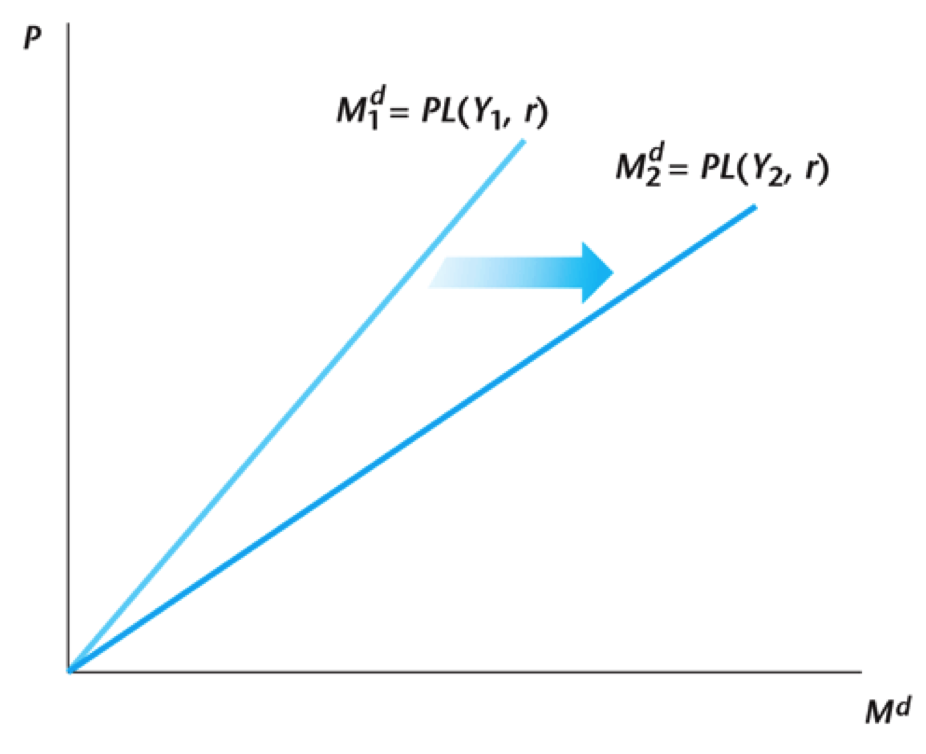
• Demand for money is then given by
$$M^d = \underbrace{P}_{\text{Price}} \times \underbrace{[Y - X^{\ast}(R)]}_{\text{Quantity}}$$
• More simply
$$M^d = P L(Y,R)$$

Demand for Money

$$M^d = P L(Y,R)$$
• Increasing in real income $Y$ – more currency required as volume of transactions increases
• Decreasing in the nominal interest rate $R$. The nominal interest rate is the opportunity cost of using currency in transactions – higher $R$ implies greater use of credit in transactions, and less use of currency
• Increasing in the price level $P$

Nominal Money Demand

• Substitute using the approximate Fisher relation
$$M^d = P L(Y,r+i)$$
• For our experiments, suppose inflation rate is zero (harmless)
$$M^d = P L(Y,r)$$

Nominal Money Demand Curve

Current Real Income

Money Supply

• In the US, the Federal Reserve (central bank) and the government are different entities
• In the model, it is convenient to assume a single institution that is in charge of both monetary and fiscal policy
$$\underbrace{P G + (1+R^{-})B^{-}}_{\text{Expenditures}} = \underbrace{P T + B + M - M^{-}}_{\text{Revenue}}$$

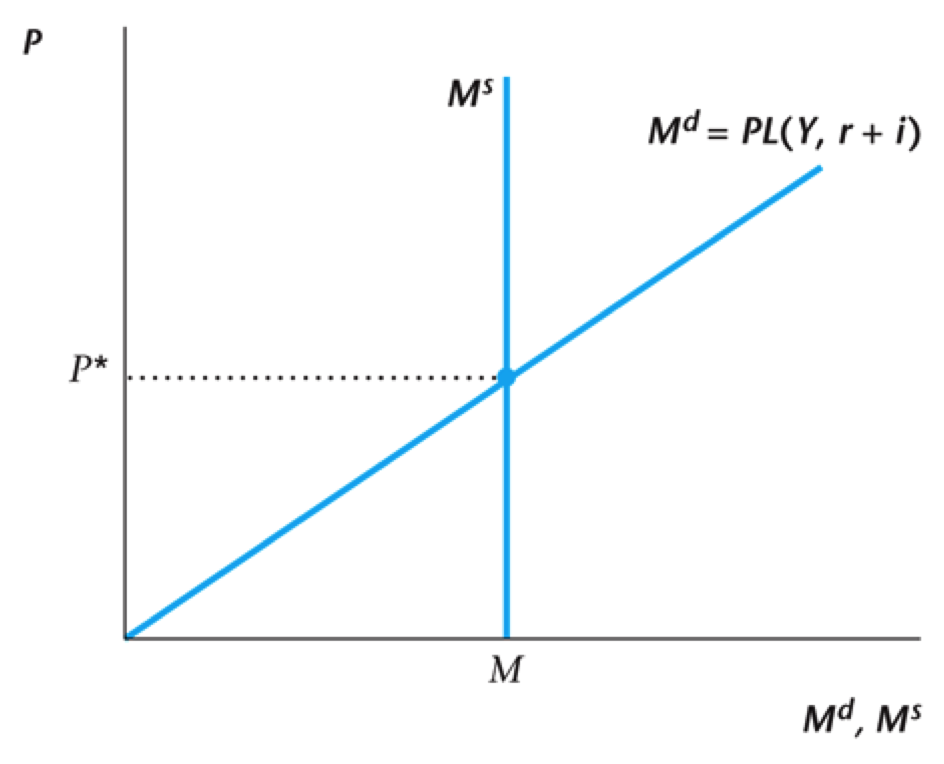
Current Money Market

Money Supply is determined by the government

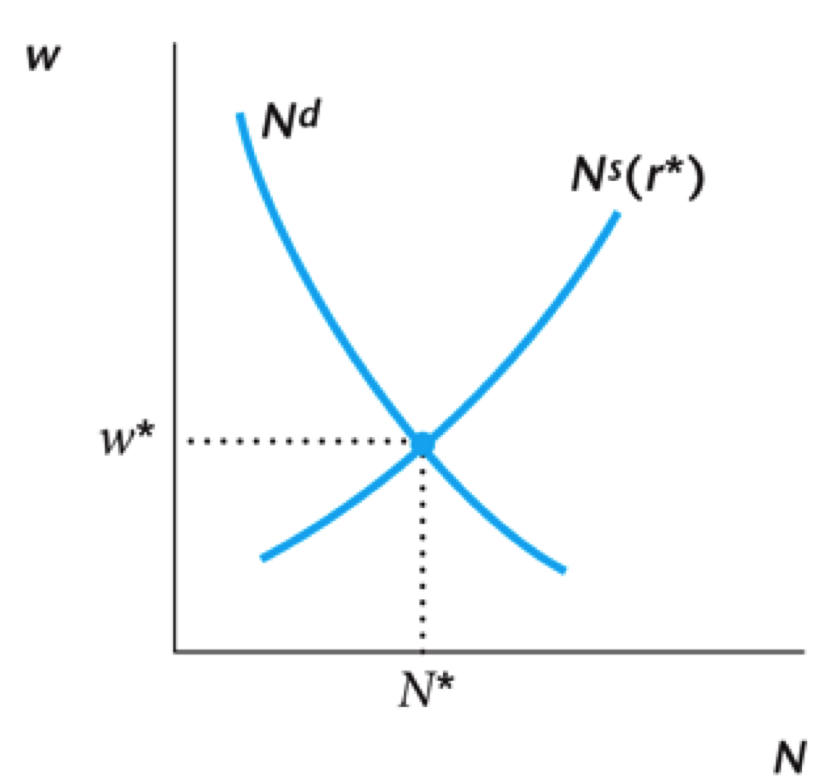
Current Labor Market

The firm's labor demand schedule is the marginal product of labor for the firm, which is downward sloping

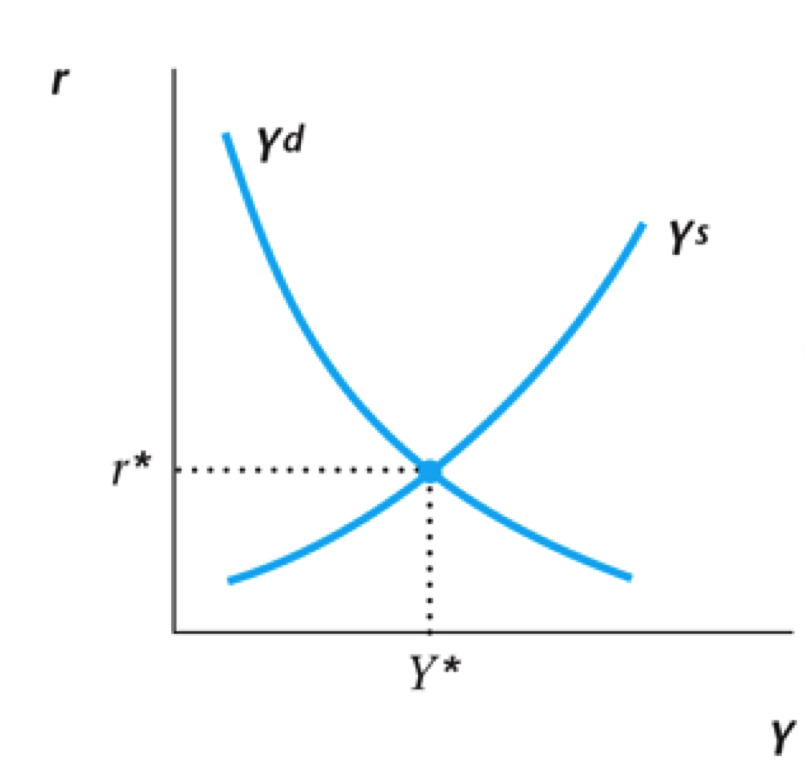
Current Goods Market

Demand and supply for current goods same last lecture

Complete Monetary Intertemporal Model

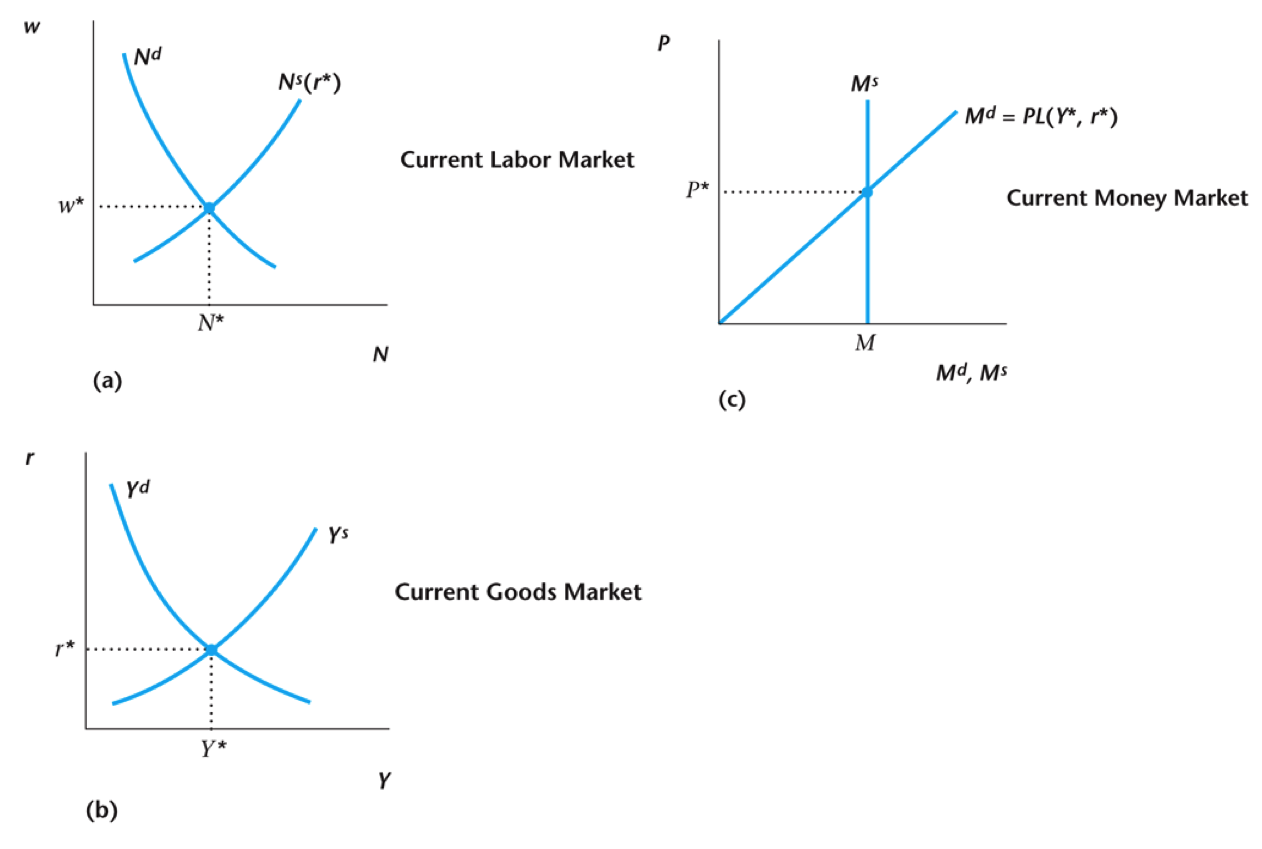
Current Money Supply

Money supply jumps up in current period (policy)

Neutrality of Money

In this model, money supply has no effect on any real macroeconomic variables

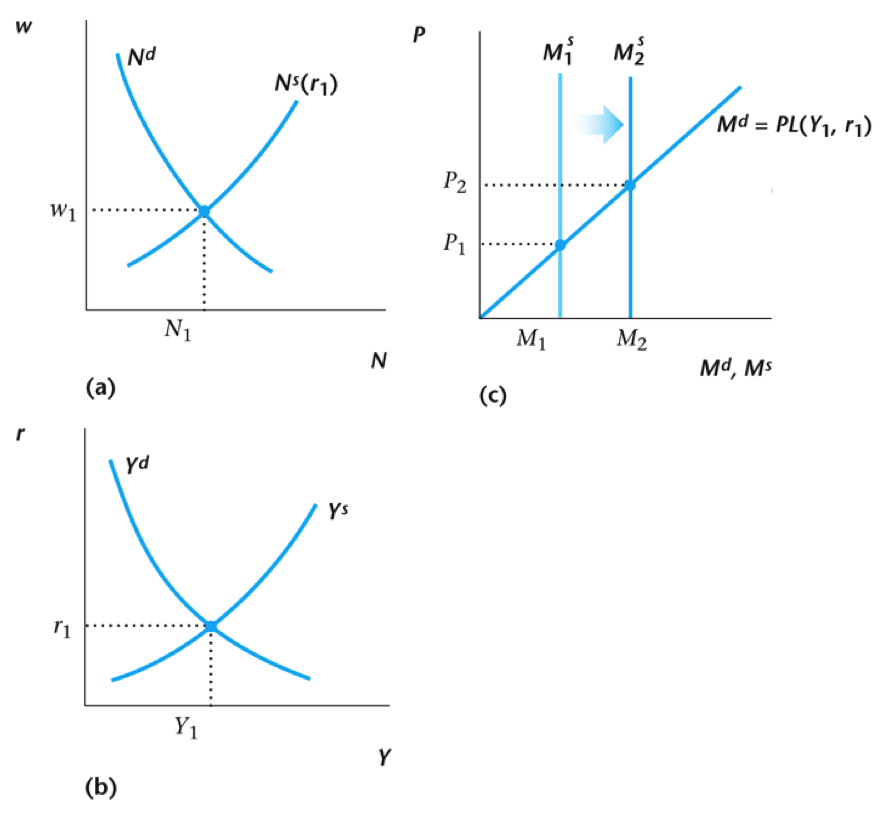
Long-run Neutrality of Money

• Economists agree that money is neutral in the long-run, later we'll look at short-run
• Shifts in the demand for money are important for how monetary policy should be conducted
• Shifts that occur within a day, week or month (the very short run) are a critical for the central bank

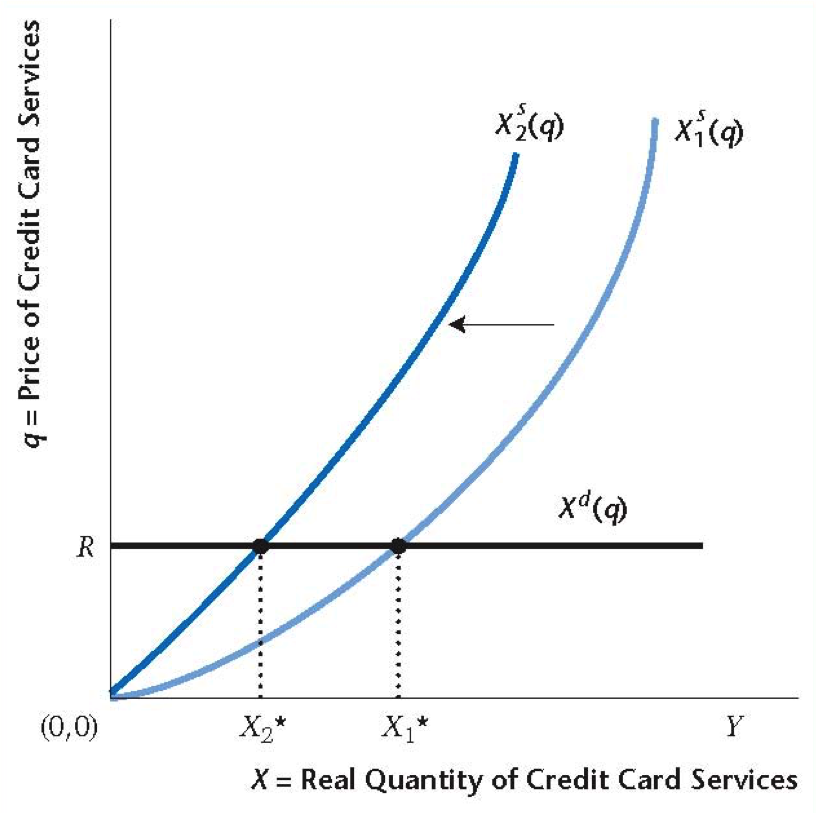
Shift in Supply of Credit

Equilibrium price does not change but quantity falls, hence demand for money increases

Shift in the Demand for Money

This leads to a decrease in the price level

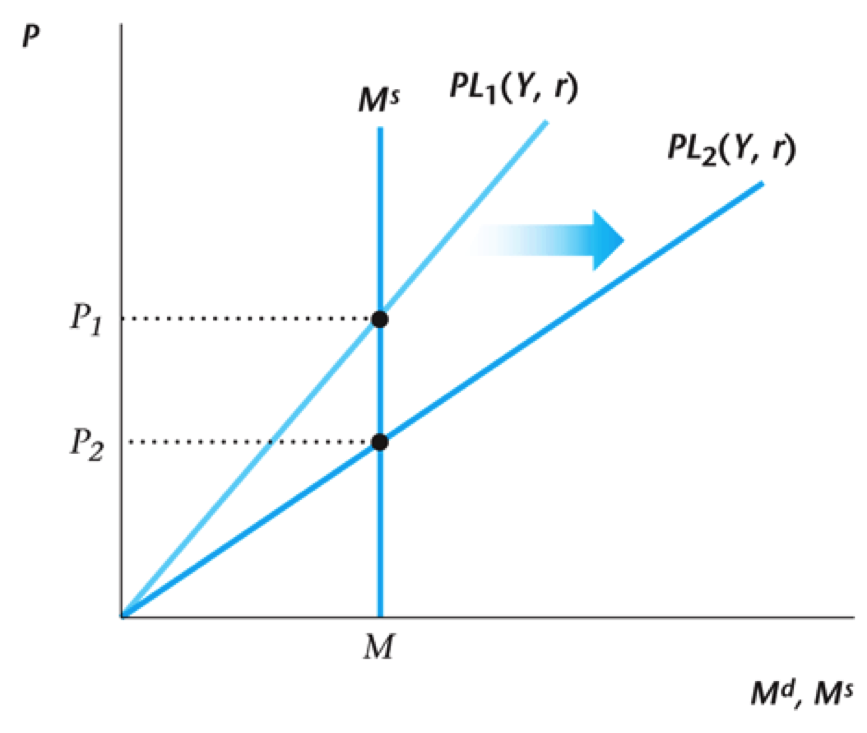
Causes of These Shifts

• New information, technologies that lower the cost of accessing bank accounts (e.g. ATM)
• New financial instruments that lower the cost of banking (e.g. checking account)
• Change in government regulations (e.g. Deposit Insurance)
• Change in the perceived riskiness of banks (e.g. bank runs during the Great Depression)

Models With Non-Neutral Money

Friedman-Lucas Money Surprise

• Imperfect information: consumers know the market nominal wage, but they do not observe all prices simultaneously, so they do not know their real wage.
• Different aggregate shocks hit the economy – money supply shocks and productivity shocks – and consumers cannot observe these shocks directly.
• When a worker sees an increase in the nominal wage, what happened to prices?

Increase in Money Supply

• Money supply increases – unanticipated and unobserved by the private sector
• Workers see an increase in their nominal wage ($W = wP$)
• Cannot tell how much real wage has increased
• Workers supply more labor, and output increases
• Nonneutrality of money, but only because people are fooled into working harder.

Effect of Increase

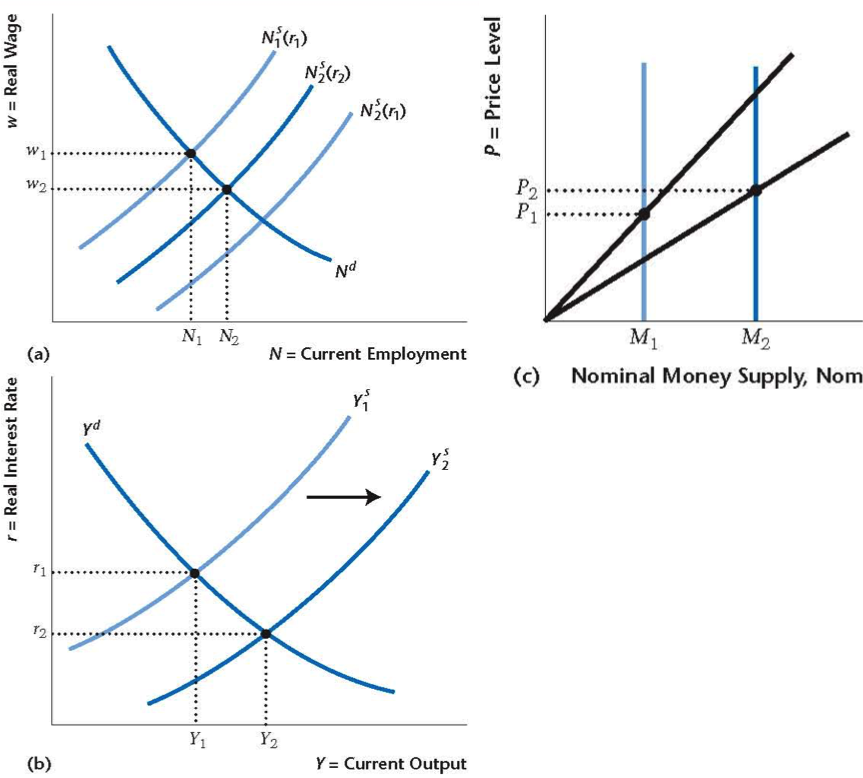
Effect of Increase

• The supply of money increases (shifts right)
• Prices and nominal wages rise, consumers think real wage has risen
• Labor supply increases (shifts right)
• Output supply increases, real interest rate falls
• Money demand increases since $M^d = P [Y-X^{\ast}(R)]$
• Non-real change induces real change $\rightarrow$ money not neutral

Role of Targeting

• Basic money surprise model seems to indicate that predictability of the money supply is good policy. (unanticipated changes in money supply result in suboptimal outcomes)
• In the model, this means a constant M. In practice it means targeting the growth rate in the quantity of money.
• This works well for productivity shocks, but not for money demand shocks.
• For money demand shocks, interest rate targeting works well.

Increase in Money Demand

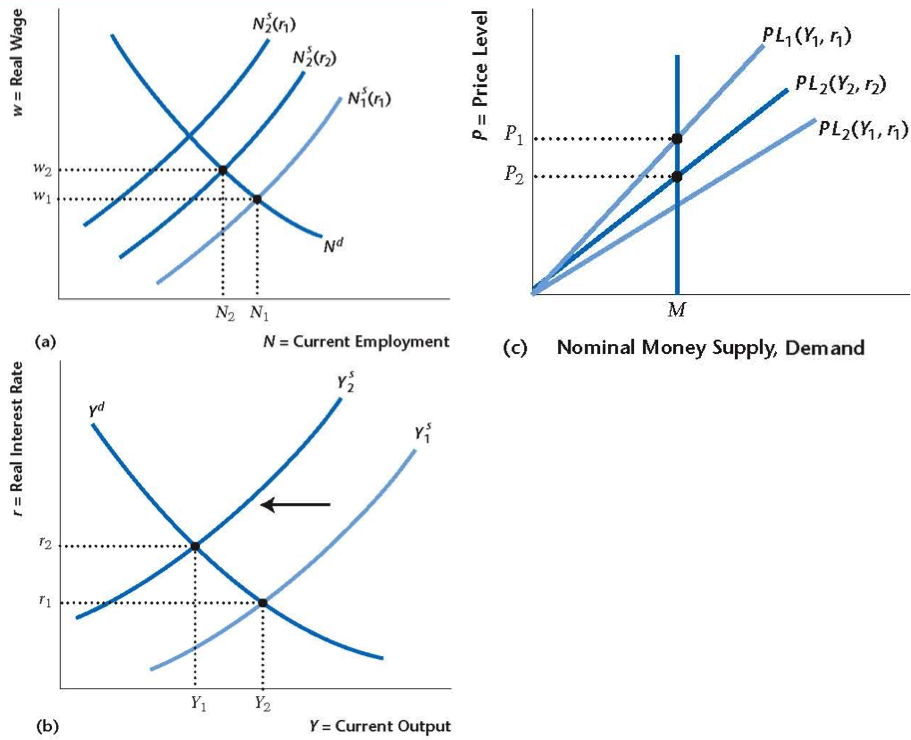
Increase in Money Demand

• Money demand rises, shifts to the right
• Prices fall to equilibrate money market $\rightarrow$ lower nominal wages
• Labor supply decreases $\rightarrow$ output supply decreases, real interest rates rise
• As a result, money demand decreases
• Money not neutral, since output drop is suboptimal

Role of Targeting

• One solution to this inefficiency could be to increase the money supply – but how can the central bank achieve this if it cannot observe the money demand shock?
• It can however observe the interest rate increase. What if the central bank instead targets the interest rate?
• Money demand $\uparrow \rightarrow r \uparrow \rightarrow$ central bank responds by increasing money supply, neutralizing the initial shock
• However, interest rate targeting can be inefficient if the shock is productivity (there no intervention would be needed)

TFP Shock with Targeting

TFP Shock with Targeting

• Negative TFP shock $\rightarrow$ labor demand decreases
• Output supply increases, real interest rates rise
• In response, the central bank decreases the money supply, decreasing prices and nominal wages
• Labor supply now decreases
• Output supply shifts back to its starting point

Desirability of Targeting

• So same output, but workers paid less $\rightarrow$ suboptimal outcome
• Over time, workers wisen up to nominal wage changes and we should return to staring wage
• An economy being hit by such shocks continually will always be a bit off

Optimal Central Banking

• What tends to work well in practice is for the central bank to target a short-term nominal interest rate in the very short run, and to consider changing this target every few weeks
• There is much volatility in money demand in the very short run – interest rate targeting accommodates this
• Productivity shocks are slower moving – the interest rate target can change in response

Alternative Monetary Policy

• Inflation targeting: Short-term interest rate target responds only to the inflation rate
• Taylor rule: Short term interest rate target responds to inflation and to real aggregate activity
• Nominal GDP targeting: central bank attempts to target nominal GDP growth (this is getting popular again)

Zero Lower Bound and QE

• QE = Quantitative Easing
• Zero lower bound: The nominal interest rate cannot go below zero, as that would imply an arbitrage opportunity: you could get paid to borrow money
• What happens when r = 0? At the zero lower bound there is a liquidity trap. Increasing the money supply through conventional means does not do anything – even prices do not change.

It's a Liquidity Trap!

It's a Liquidity Trap!

• When there is a liquidity trap, think of money demand being inelastic to the price level
• Increasing money supply has no effect, not even on prices
• In a liquidity trap, government bonds (with close to 0 interest) and money are essentially identical

Quantitative Easing

• Under conventional accommodative monetary policy, the central bank swaps money for short-term government securities.
• But in a liquidity trap, this does not do anything.
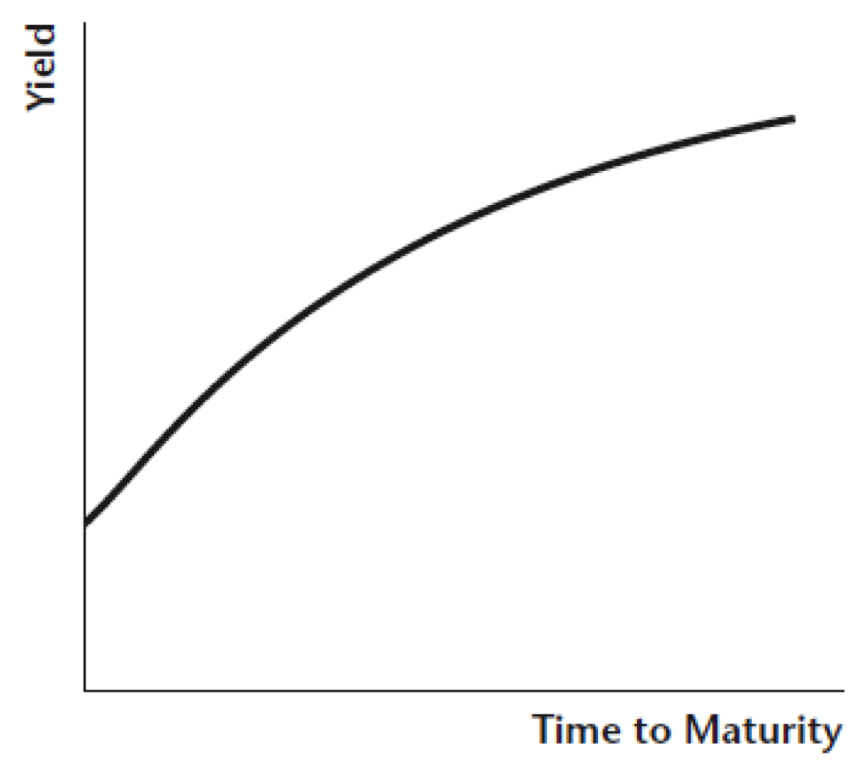
• However, long-term nominal interest rates can be positive when short rates are zero.
• What if the central bank purchases long-term government securities? Won’t long-term interest rates go down?

Typical Yield Curve

Does QE Work?

• Tried in the United States and in the U.K., post-financial crisis.
• Swaps of money for long-term government bonds and other long-term assets.
• Central bank hopes that this reduces long-term interest rates.
• Possibly, it does not. Does the central bank have an advantage, in a liquidity trap, in turning long-maturity government bonds into short-term liquid assets?
• Mortgage rates have been historically low...
• More research needs to be done.

Ben Bernanke Has a Blog!

The Ben Bernank

Janet Yellen

Addendum: Bitcoin

Bitcoin

A cryptographic currency developed by "Satoshi Nakamoto", an unknown person or group of researchers

Basic Concepts

• Bitcoin: unit of electronic currency, can be exchanged like any other commodity or currency
• Block chain: public ledger keeping track of all transactions in an ordered manner

Infrastructure

• Distributed: transactions are announced publicly, then collected and continually verified
• Why verify? Same reason to verify hard currency - wouldn't want to end up with a counterfeit bitcoin
• There are also ways to include a transaction fee, which is basically a bonus paid to people that verify your transactions

Mechanism

• Why not announce Alice gives 100,000 BTC to me today? You can't - you need to know Alice's private key, basically a password
• Security mechanism: cryptography. With her private key, Alice can generate a valid transaction that can be verified with her public key. Nearly impossible to generate valid transaction originating from Alice's address without her private key.

Cryptography

Public key: 34 characters starting with 1 or 3, represents an address and is used to verify transactions from that address

16UwLL9Risc3QfPqBUvKofHmBQ7wMtjvM

Private key: 51 characters starting with 5, used to generate transactions from that address

5Kb8kLf9zgWQnogidDA76MzPL6TsZZY36hWXMssSzNydYXYB9KF

Underlying Mechanics

• Cryptography relies on functions that are easy to compute (or verify) but difficult to invert
• Like currency: easier to verify authenticity of $100 bill than to create one

Cyptographic Signature

• If Alice wants to send Bob $100: encode details in number "Trans"
$$TID = f(Trans,APriv)$$
• Private key and public key are made so that
$$g(TID,APub) = Trans$$
• The function $g$ is easy to compute (so as to verify transaction), but hard to find $TID$ for some random $Trans$

Implementation

• Anonymous: nothing intrinsically tying people or places to bitcoin addresses. Control of address is determined by knowledge of private key.
• Analogy: each address is like a safe and the owner has the key. Transactions move gold between safes, you only need key to origin safe (not destination, like library drop-off box?)

Money Supply

• Bitcoins are created when "miners" discover new ones by undertaking computation
• Difficulty of mining is designed to increase without bound as number of bitcoins approaches 21 million, so that's the max
• Right now, there are about 14 million

Number of Bitcoins Over Time

Transaction Fees

• Any transaction says something like (1) Take $X$ BTC from Alice, (2) Give $Y$ BTC to Bob
• Miners then pick these up and verify them, which makes the transaction official in some sense
• If $Y \lt X$, the miner is free to assign the transaction fee $T = X - Y$ to themselves
• Large transaction fees will attract miners. Transaction fees are currently voluntary, kind of like tipping

Incentives for Verification

• Right now miners are incentivized to find new coins and in the process verify the blockchain
• When new coins run out, they can still get by on transaction fees
• Fees are provided voluntarily, so at some point verification will become like a public good whose provision is enforced by norms (possibly problematic)

Mapping to Our Environment

• Transaction fees are like $q$, but chosen by users (a "bounty" for verification)
• Higher transaction fees attract more miners, meaning there can be more Bitcoin services and a larger supply of Bitcoin transactions (and incidentally more actual Bitcoins, at least for the next few years)
• Bitcoin algorithm is tuned to create a new block about once every ten minutes, this is like the heartbeat of the bitcoin network

Price Volatility

• Bitcoin has volatility approximately 8 times higher than USD
• Might be due to uncertainty about long-term value? Do people believe that Bitcoin really works?
• What if quantum computing is successfully realized? That would wreak havoc on Bitcoin, amongst many other systems.

Bitcoin Price

Bitcoin Price Volatility

Transaction Fees

Credit Services Provision

• Now we have two instruments: bitcoin and credit
• Credit services have service fees $q$ and bitcoin has transaction fees $t$
• In old model, cash had no transaction fees ($t=0$), but in reality cash might have higher transaction fees than bitcoin
• Can think about bitcoin as negative shock to $t$

Credit Services Equilibrium

• Let $X^b(t)$ and $X^c(q)$ be supply of bitcoin and credit services
$$Y = X_b(t) + X_c(q)$$
• In order to make consumer indifferent between bitcoin and credit
$$R + t = q$$
• Holding bitcoin means money is not in bank earning $R$ interest

Visualizing the Equilibrium

Effect of Introduction

• Introducing bitcoin lowers transaction costs of cash instrument
• This means higher supply of cash for same $t$, supply curve shifts out
• Result is less usage of credit services and lower credit fees

General Model

• Can also think of a three-type model: USD, BTC, credit
• Introduction and adoption of Bitcoin could represent a shock to USD demand